South Korean Growth: A Case Study Using The Solow & Mankiw-Romer-Weil Models

Introduction

In examining the dynamics of long run growth in the South Korean economy from 1950 to 2020, there are two models to be applied: the Solow model, and the Mankiw, Romer & Weil (MRW) model, otherwise known as the Human Capital Augmented Solow (HCAS) Model. These models offer valuable insights for understanding the interplay between capital, technological progress, population growth and other relevant variables, and in the case of MRW, the crucial role of human capital in driving economic development. 

Models & Application

The Solow Model is seen as the “workhorse” for the neoclassical model of economic growth, and what makes this model unique is that it describes the economy dynamically. Being a dynamic model, it is possible to investigate beyond the balanced growth path or the steady-state equilibriums, but the process of how an economy moves to these points.

Figure 1: Log Output per effective worker, compared with the MRW Model and the Solow Model, both in logs. Data sourced from the World Bank

Figure 1 illustrates the comparison of the Solow model and MRW model against log output per unit of effective worker, log(Y/L). While both models exhibit a degree of similarity with the statistic, the MRW model emerges as the more appropriate model for describing the South Korean economy, displaying almost identical Output since records began.

Furthermore, in motivating the use of the MRW model, it is important to explore into the model’s underlying intuition. The MRW model accounts for much of the observed differences that physical capital fails to capture, prompting the inclusion of human capital to account for these variations. Human capital, similar to physical capital, can accumulate through education or in ‘learn-by-doing’ environments. As a result of these factors, the MRW model assumes a more prominent role for analysis. The above graphic is derived from the aggregate production functions from both models, each assumed to be a Cobb-Douglas function, detailed below:

Aggregate production function for MRW:

Aggregate production function for Solow:

Additionally, a critical condition within the MRW framework stipulates that α > 0, β > 0, α + β < 1. This condition holds significant importance as it ensures that the model remains applicable. By imposing this condition, the model guarantees constant returns to scale, and thus allowing for the assumption of a balanced growth path. While Solow does not feature the condition for β, it must also remain in a similar state.

Shifting focus from output, physical and human capital can be characterised by separate loci, described by their respective fundamental laws of motion. Any deviation from these functions will impact the respective capital per unit of effective labour and the equilibrium as a result.

When observing deviations from the locus of human capital, a shift to the left indicates that actual investment becomes greater than break-even investment, resulting in a positive accumulation of human capital per unit of effective labour. Conversely, a deviation to the right of this locus indicates that actual investment is less than break-even, resulting in a negative accumulation.

Physical capital features similar consequences, to move about the locus means that actual investment is less than break-even investment, resulting in a negative accumulation of physical capital per effective unit of labour. Conversely, a move below this locus means that actual investment is greater than break-even, resulting in a positive accumulation. Below is the functions for the respective loci:

Fundamental law of motion – Physical Capital:

Fundamental law of motion – Human Capital:

Figure 2: The dynamics of physical & human capital per unit of effective labour, with a shift in human capital.

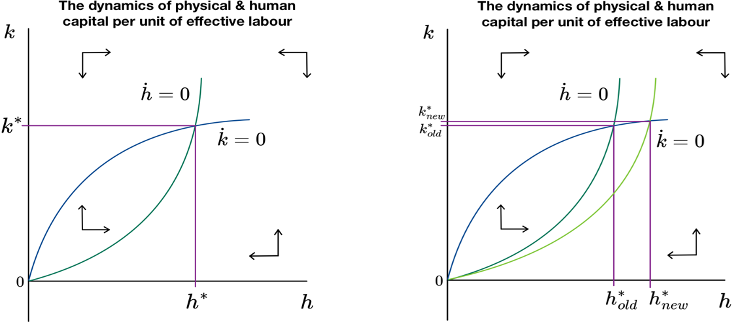
While output per effective worker is not explicitly represented on either axis of the phase diagram, it is still crucial for interpreting the level of output within the model. Assuming the economy is on a balanced growth path, where steady states k* and h*  exist, and that a significant and permanent increase in the rate of savings allocated to human capital  (such as government expenditure on education) takes place. This can lead to a direct impact on the human capital locus, establishing a new steady state h*. The model then predicts that a new k* is then set indirectly, as the new intersection is higher than the previous. This shift in both the theoretical  and  can be seen in the data.

Figure 3: Log Government expenditure on education () and Capital stock per Capita (KL)

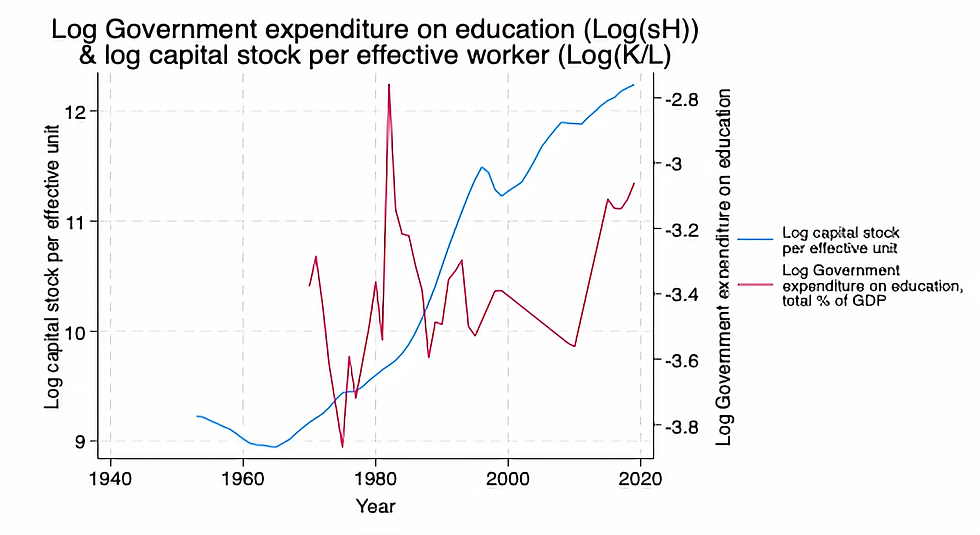
However, this indirect impact on k* does not manifest for several years and only experiences a large increase once s_H moves beyond approximately 3% of total GDP. Furthermore, capital stocks appears to be rather sensitive to this spending on education, with additional percentage points resulting in massive increases in capital stocks, as shown above in figure 3.

Figure 4: Output (Y/L) and Capital (K), before and after an increase in s_H

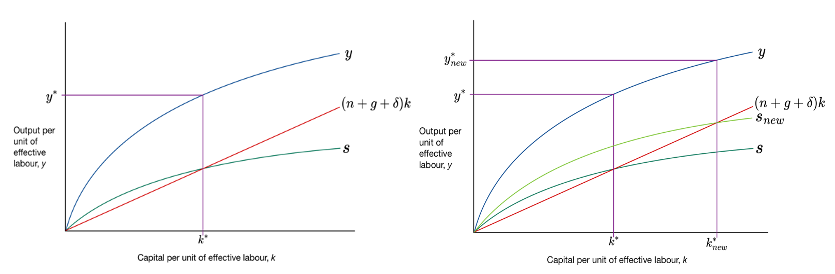
A comparison between figure 1 and figure 4 illustrates the impact of an increase in s_H. The transition from k*(old) to k*(new)  observed in figure 4 is accompanied by the corresponding increase in log output per unit of effective labour, log(Y/L) , aligning with the theoretical shift from y*(old) to y*(new)  in that an increase of human capital allows for a more educated population who can engage with technology and other means more effectively.

Figure 5: Technology Growth and Population Growth, side by side.

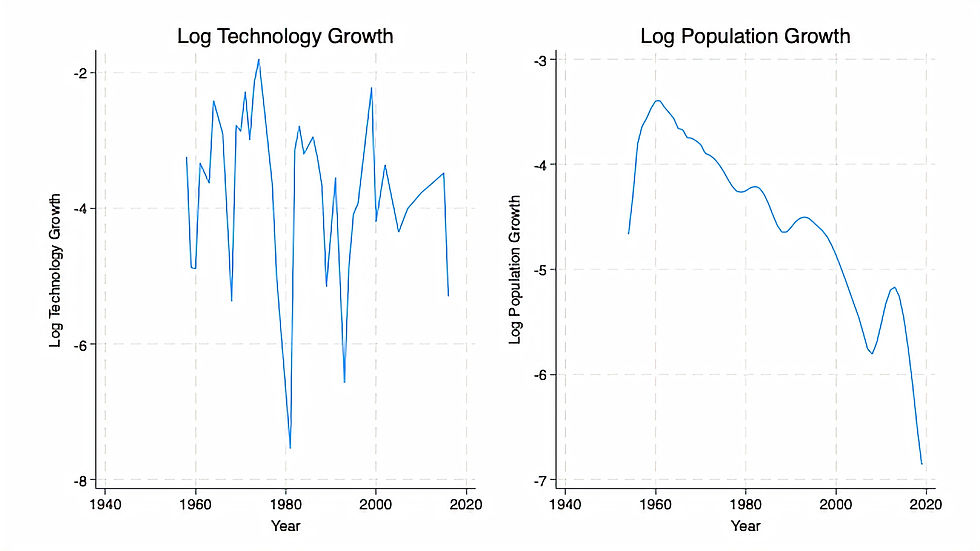
Both technology and population growth feature a negative trend in the data, indicating that their influence on the South Korean economy is decreasing and having a diminishing effect on output per unit of effective labour, using the fundamental law of motion, with physical capital as an example:

The decline in both parameters impacts the second part of this equation, , which represents break-even investment. This decline indicates that capital  is less influential on its own, with the output increasingly dependent on other parameters, such as saving rates and human capital.

Figure 6: Output (Y/L) and Capital (K), before and after a decrease in n & g

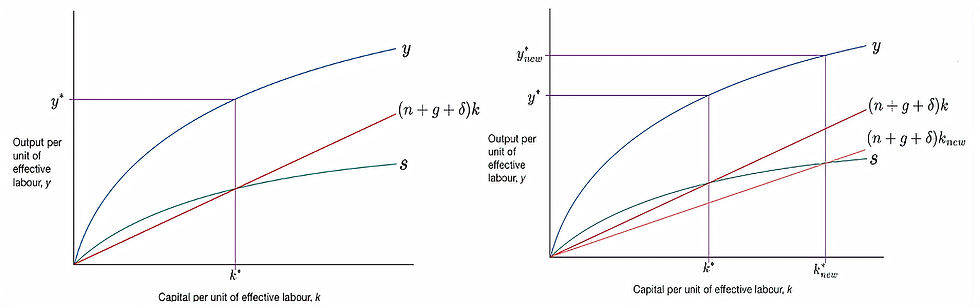
Using figure 6, a substantial and permanent decline in both the growth rate of technology and the growth rate of population can be mapped within the (n+g)k_t portion of the fundamental law of motion.

A comparison between figure 1 and figure 6 illustrates the impact of a decrease in (n+g)k_t. The transition from k*(old) to k*(new) observed in figure 6 is accompanied by the corresponding increase in output per unit of effective labour, Y/L, aligning with the theoretical shift from y*(old) to y*(new) in that while both growth rates have slowed down, this indicates workers have access to a more appropriate number of units of technology to produce output. This is in contrast to an early population boom in the late 1950s to early 1960s, with technology only catching up in the late 1970s, indicating that there may have been too little units of technology to be effective with workers.

Limitations of the Models

While both the Solow and MRW models have proven effective in describing the South Korean economy, they are not without criticism. These models rely on several assumptions that, while simplifying the modelling process, do not align with the complexities of the actual economy.

Firstly, these models assume a closed economy, disregarding the extensive trading presence that characterises the South Korean economy, which is heavily integrated into trading networks globally.  Furthermore, the assumption of a lack of government intervention is unrealistic, given the South Korea’s government active involvement, particularly in areas such as education for improving human capital (as observed in figure 3).

Additionally, the models presume identical households and firms, that can be abstracted to a single representative unit, overlooking the inherent diverse socioeconomic landscape in South Korea. Moreover, the assumption of firms producing a single good fails to capture the diverse range of goods and services produced by the major industries within the South Korea economy.

As a consequence of these assumptions, certain data points remain unaccounted for, falling outwith the scope of these growth models.

Conclusion

Through examination of the Solow and MRW growth models by using data from the South Korean economy from 1950 to 2020. It is understood that both of these models can be effective, with MRW being more appropriate at describing the South Korean economy than the Solow model, through examining output per effective worker, human and physical capital and the growth rates of technology and population through both theoretical and graphic means.

However, it is important to acknowledge that these models, while descriptive, are inherently limited by their assumptions and abstraction of economic agents. As shown in figure 1, some data remains unexplained and outwith the models, and thus exogenous, highlighting the inherent complexities of real economies that models such as Solow and Mankiw-Romer-Weil do not capture.